Download pdf

Journal link

HAL Link

ARXIV Link

Authors: A. Griffin, S. Nazarenko, V. Shukla, M.-E. Brachet

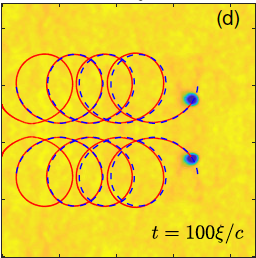
Abstract

We study the existence and uniqueness of solution to stochastic porous media equations with divergence Itô noise in infinite dimensions. The first result prove existence of a stochastic strong solution and it is essentially based on the non-local character of the noise. The second result proves existence of at least one martingale solution for the critical case corresponding to the Dirac distribution.Experimentalists use particles as tracers in liquid helium. The intrusive effects of particles on the dynamics of vortices remain poorly understood. We implement a study of how basic well understood vortex states, such as a propagating pair of oppositely signed vortices, change in the presence of particles by using a simple model based on the Magnus force. We focus on the 2D case, and compare the analytic and semi-analytic model with simulations of the Gross-Pitaevskii (GP) equation with particles modelled by dynamic external potentials. The results confirm that the Magnus force model is an effective way to approximate vortex-particle motion either with closed-form simplified solutions or with a more accurate numerically solvable ordinary differential equations (ODEs). Furthermore, we increase the complexity of the vortex states and show that the suggested semi-analytical model remains robust in capturing the dynamics observed in the GP simulations.