Download preprint-pdf
Authors
G. Sadaka, V. Kalt, I. Danaila and F. Hecht
Abstract
We present a finite element toolbox for the computation of Bogoliubov-de Gennes modes used to assess the linear stability of stationary solutions of the Gross-Pitaevskii (GP) equation. Applications concern one (single GP equation) or two-component (a system of coupled GP equations) Bose-Einstein condensates in one, two and three dimensions of space. An implementation using the free software \ff is distributed with this paper. For the computation of the GP stationary (complex or real) solutions we use a Newton algorithm coupled with a continuation method exploring the parameter space (the chemical potential or the interaction constant). Bogoliubov-de Gennes equations are then solved using dedicated libraries for the associated eigenvalue problem. Mesh adaptivity is proved to considerably reduce the computational time for cases implying complex vortex states. Programs are validated through comparisons with known theoretical results for simple cases and numerical results reported in the literature.
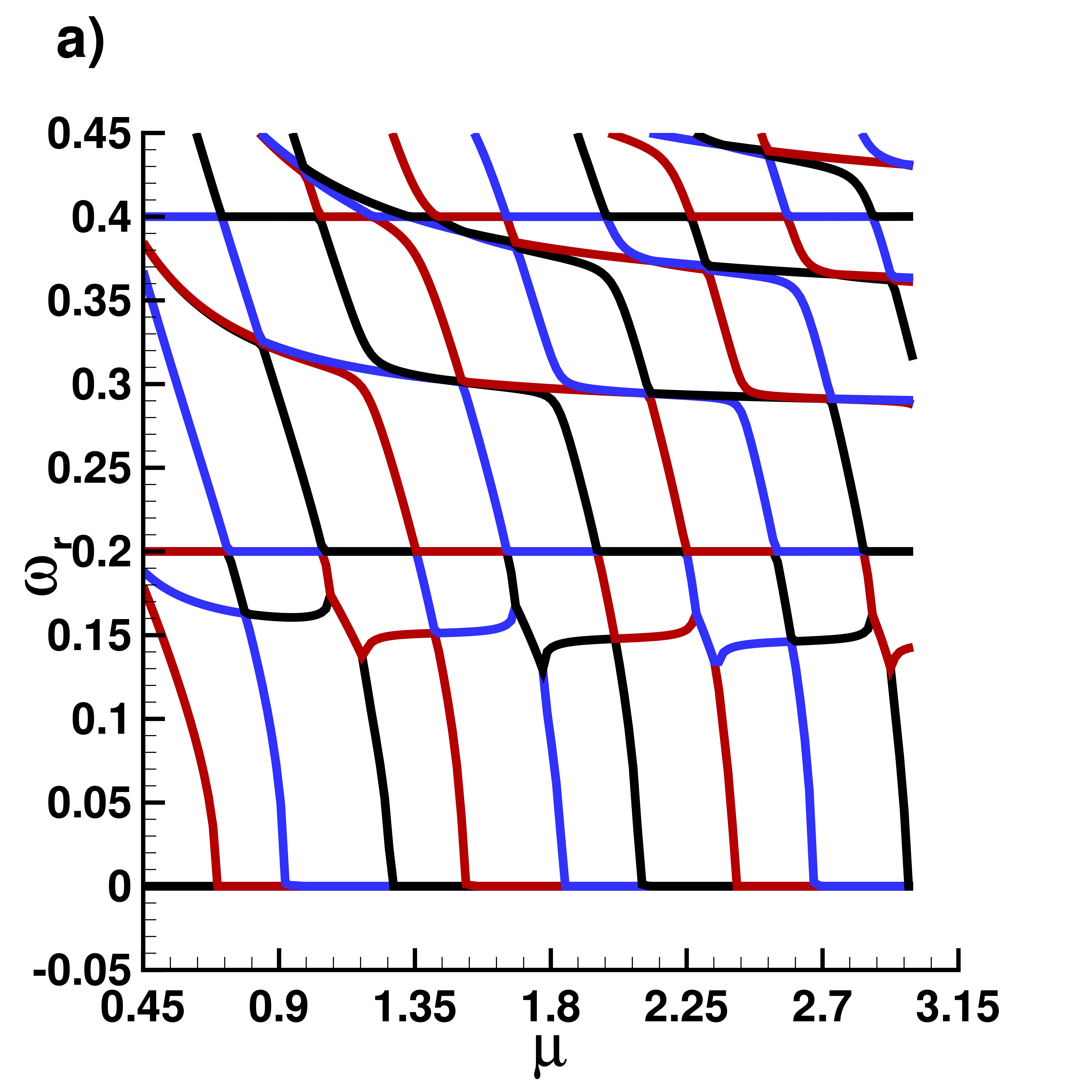
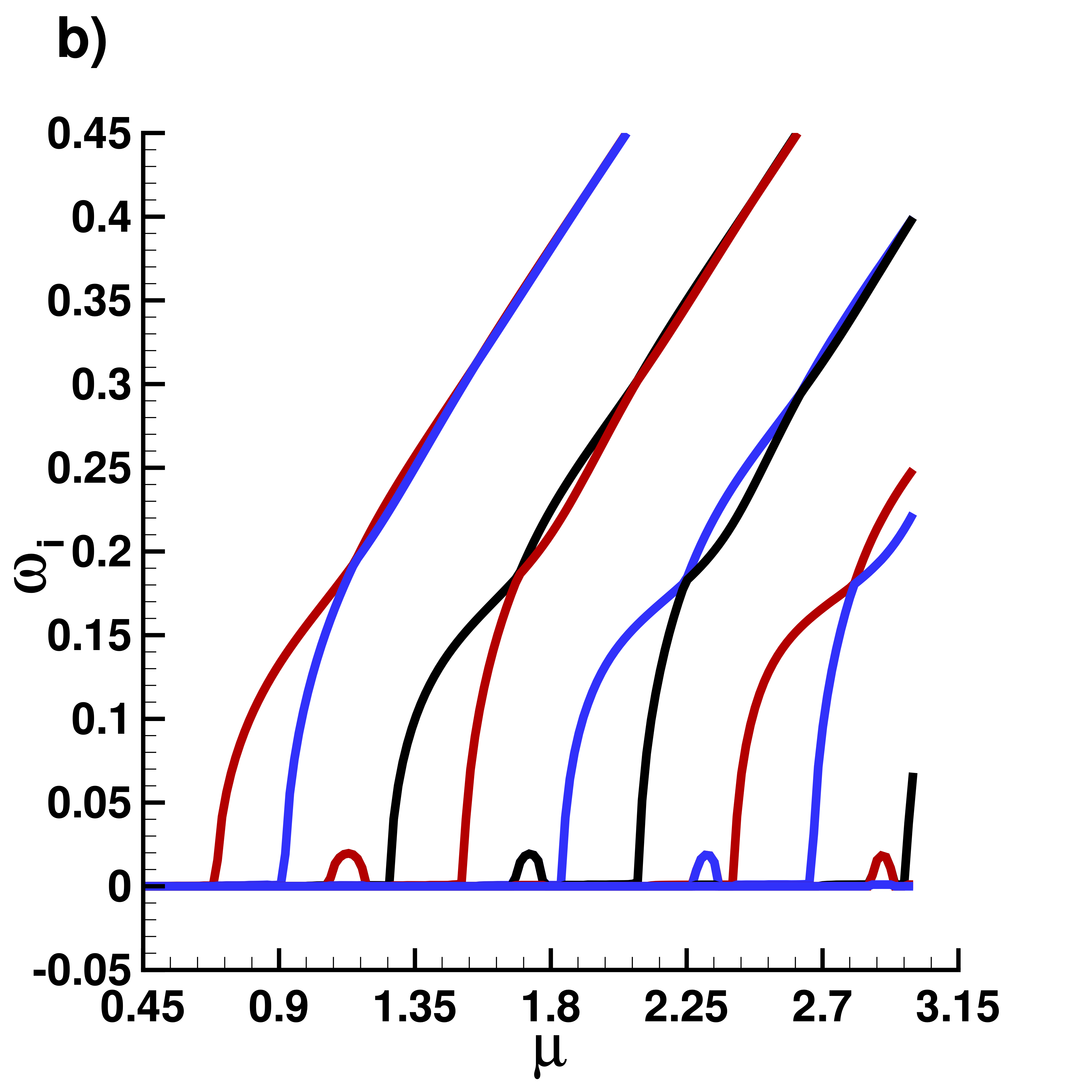
Supplemental material: 2D centered dark soliton case
Snapshots of the solution for $\mu=3$
 |
Real part $\omega_r$ of eigenvalues
 |
Imaginary part $\omega_i$ of eigenvalues
 |
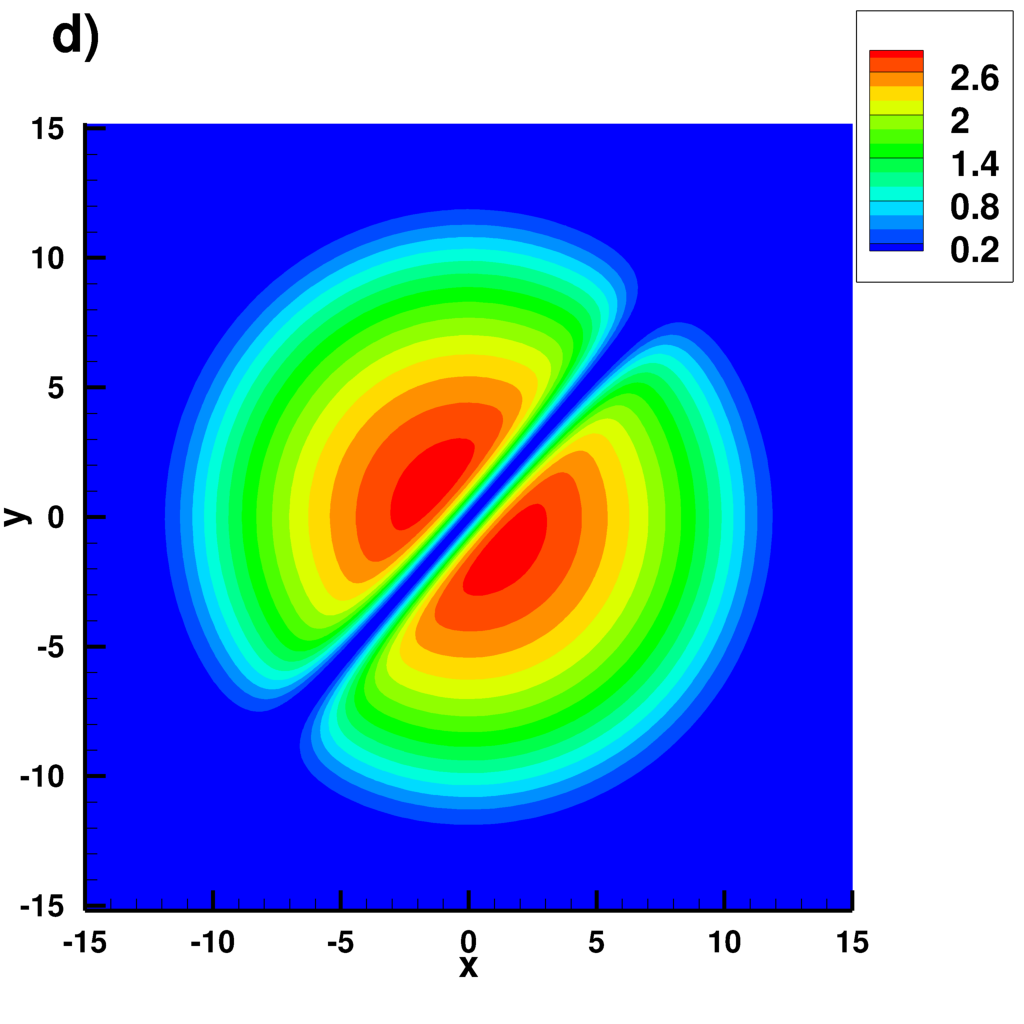
Supplemental material: 2D central vortex case
Snapshots of the solution
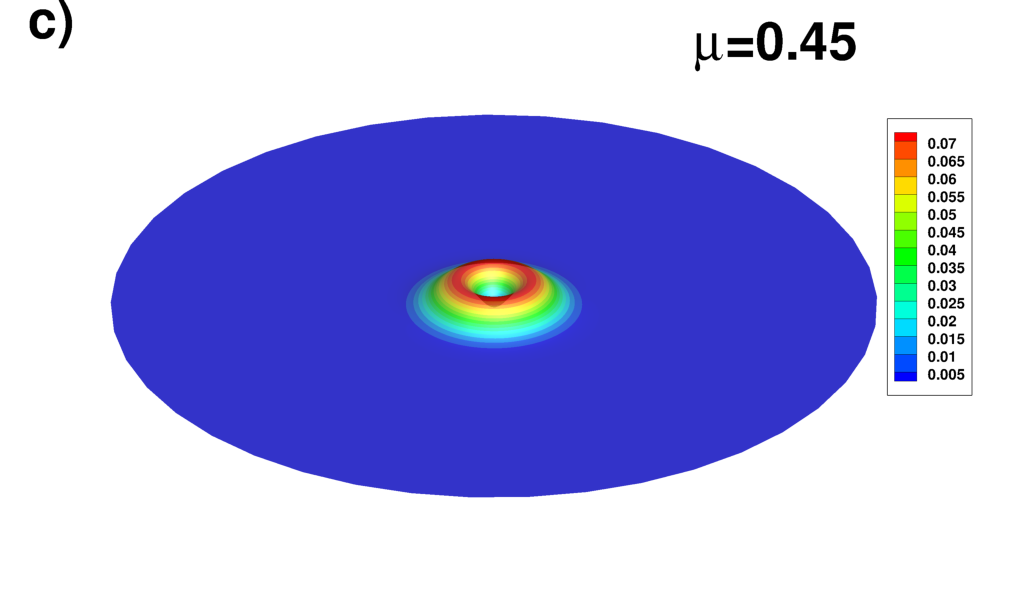 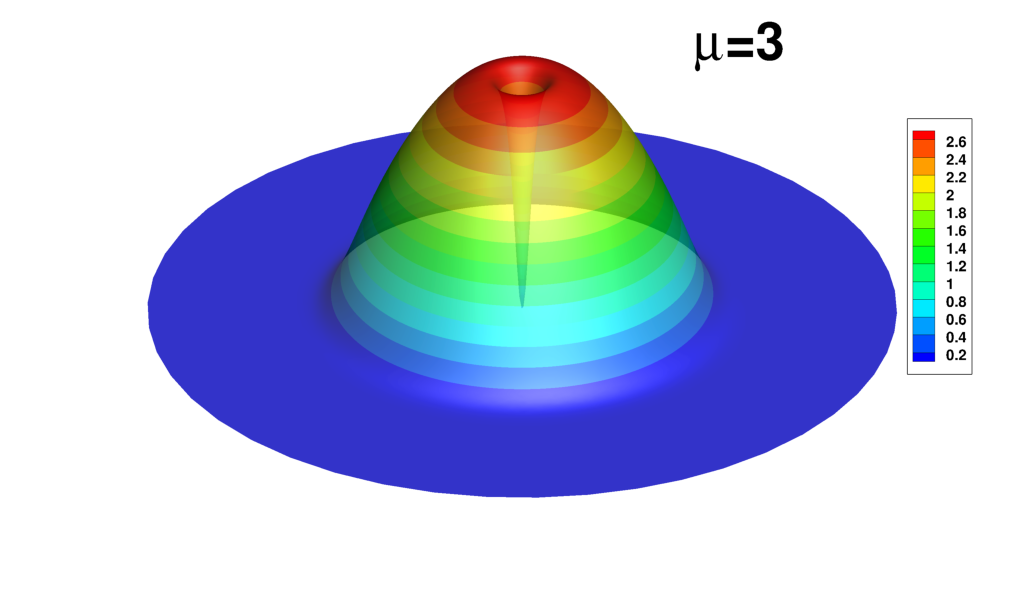 |
Real part $\omega_r$ of eigenvalues without mesh adaptation
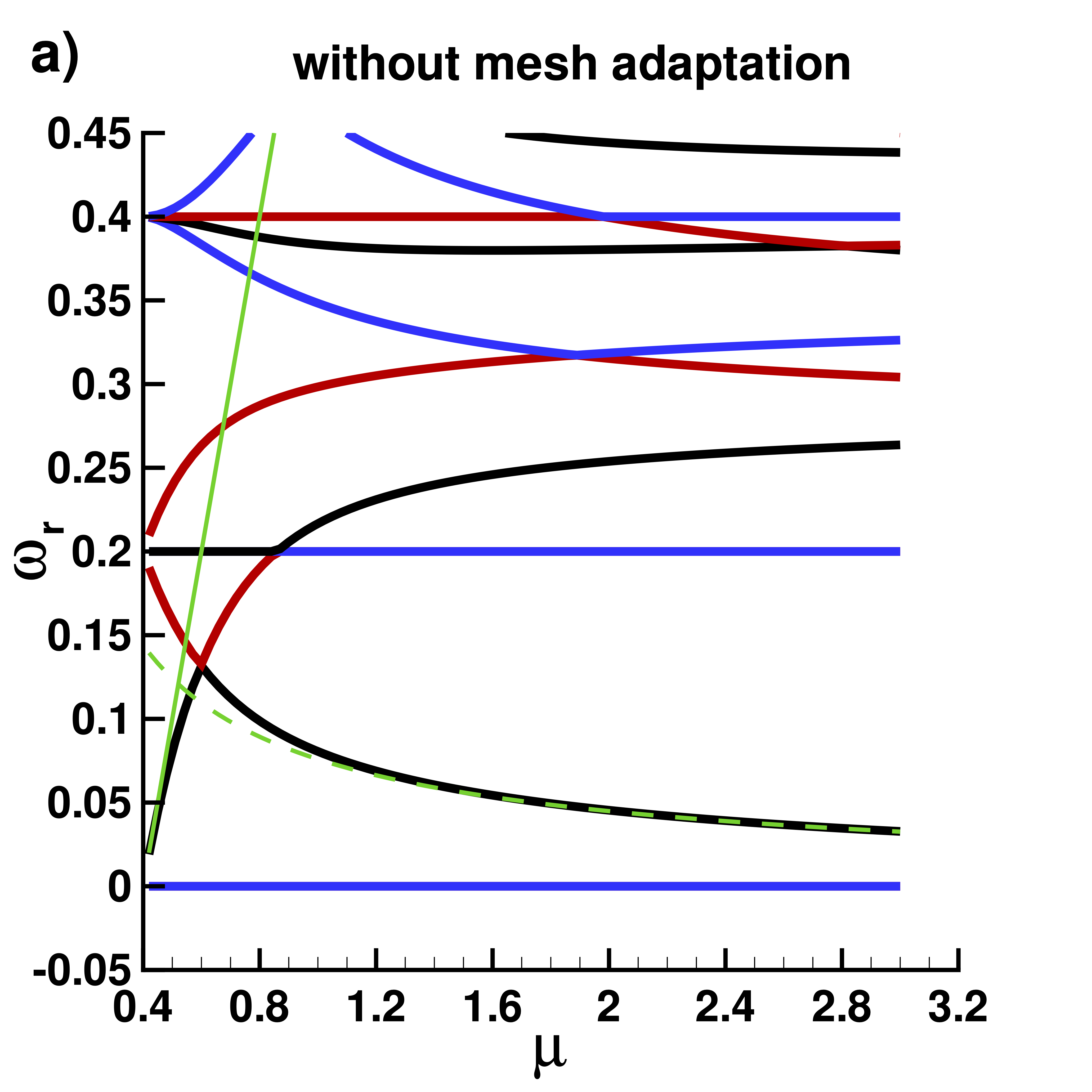 |
Real part $\omega_r$ of eigenvalues with mesh adaptation
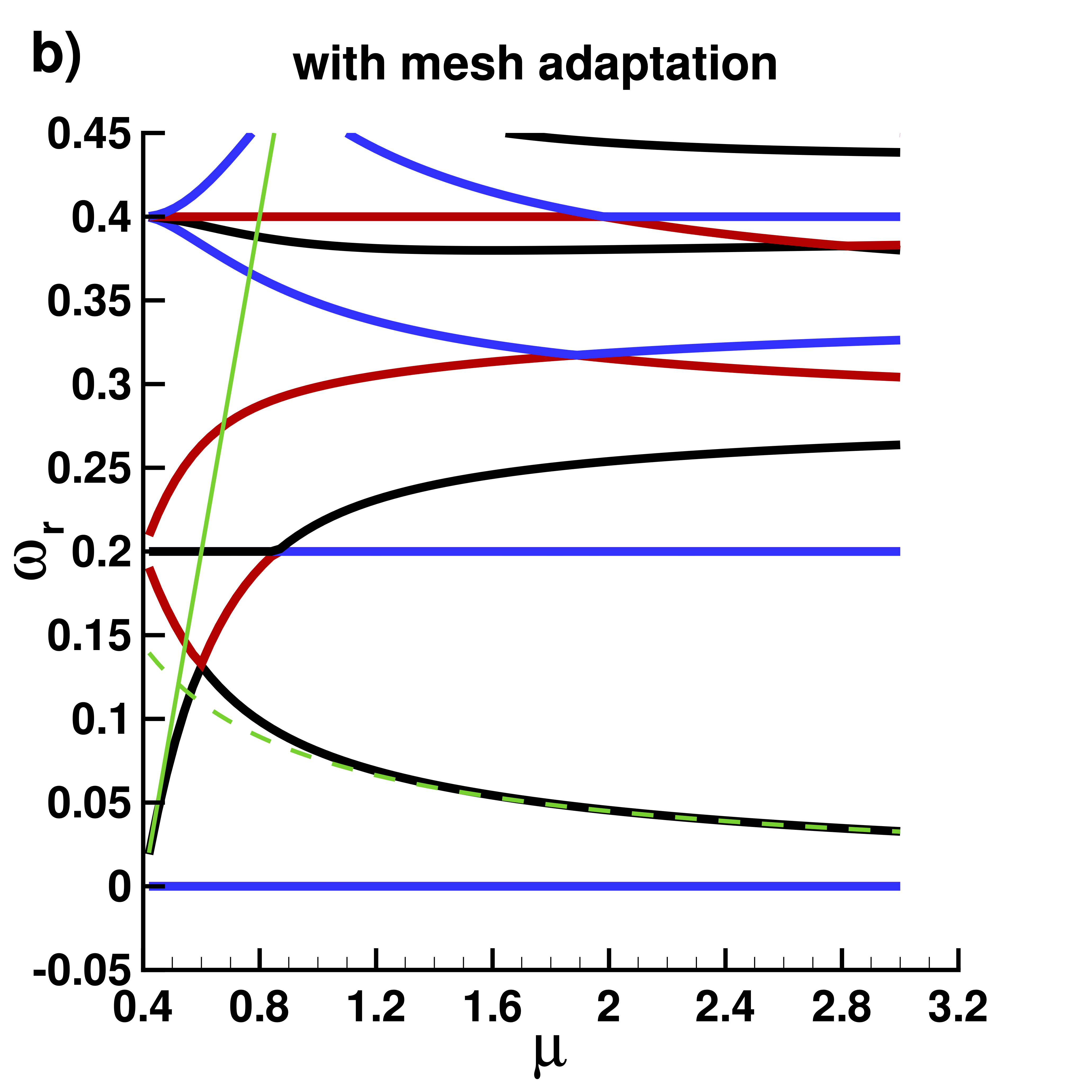 |
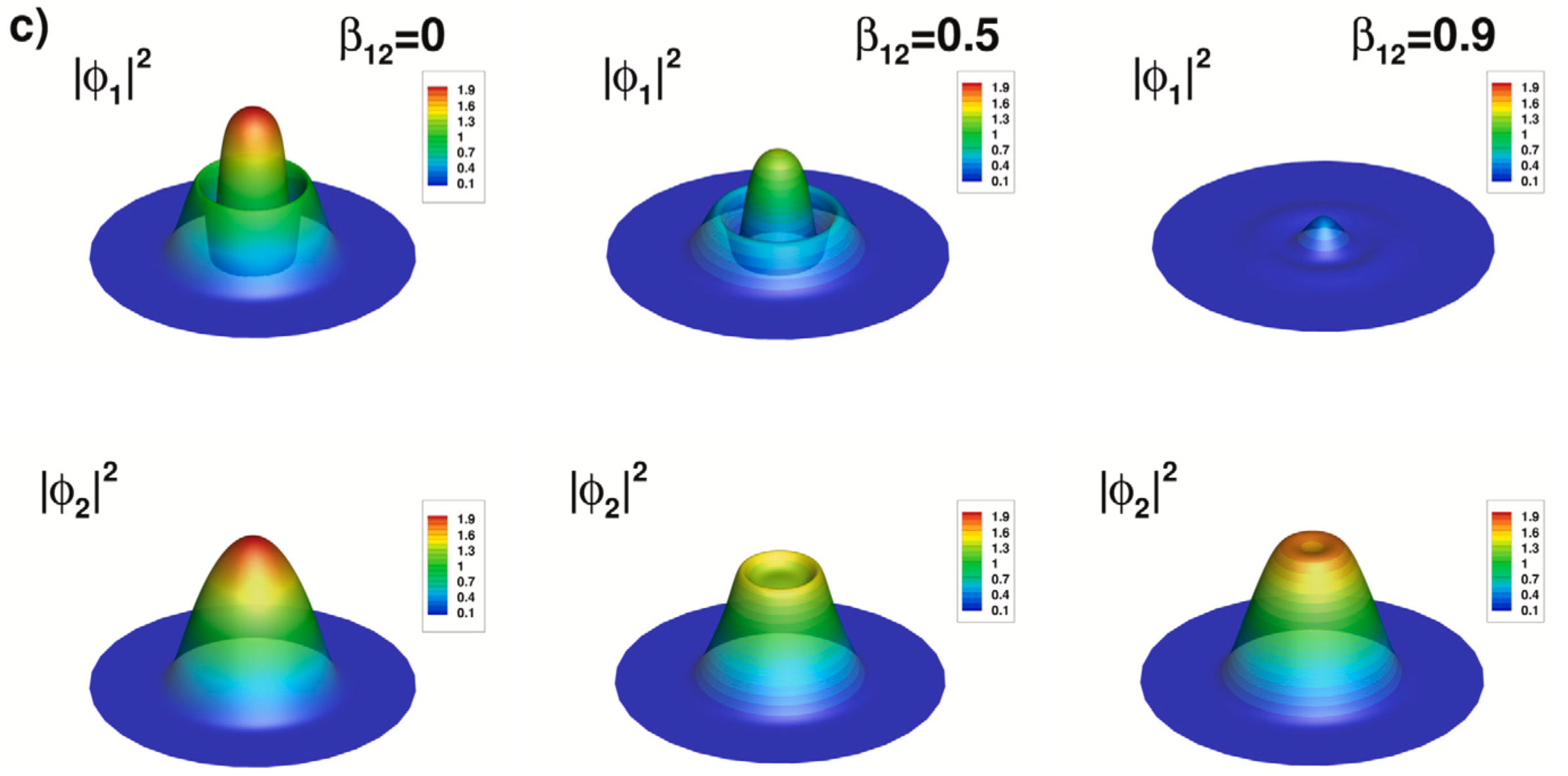
Supplemental material: 2D ring-antidark-ring state case
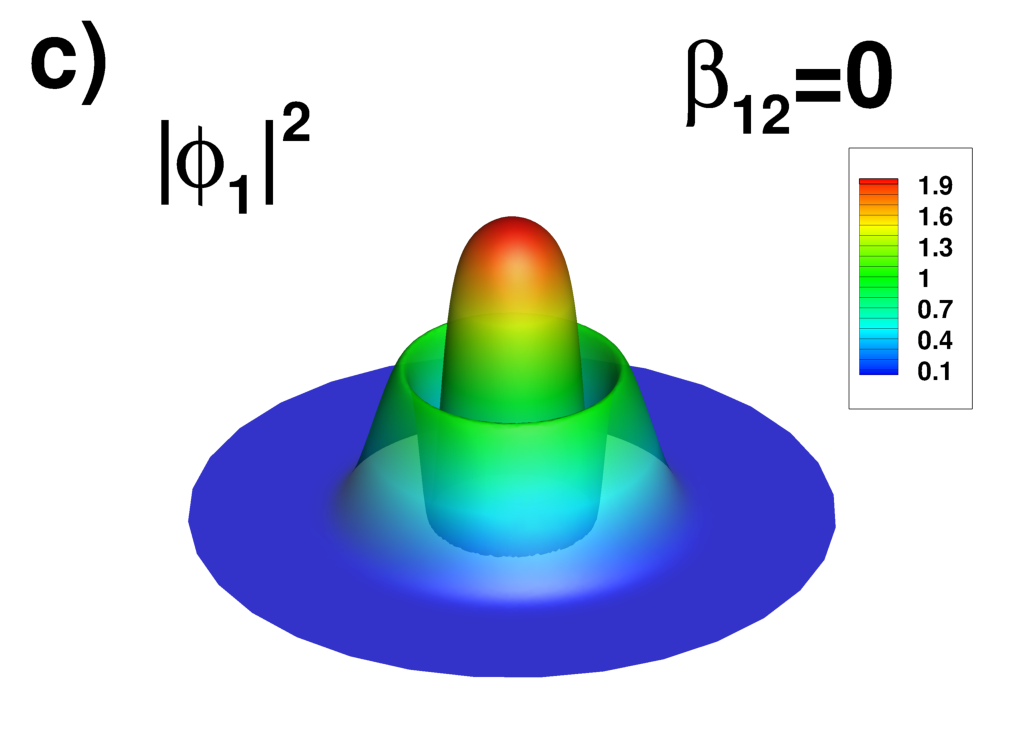 |
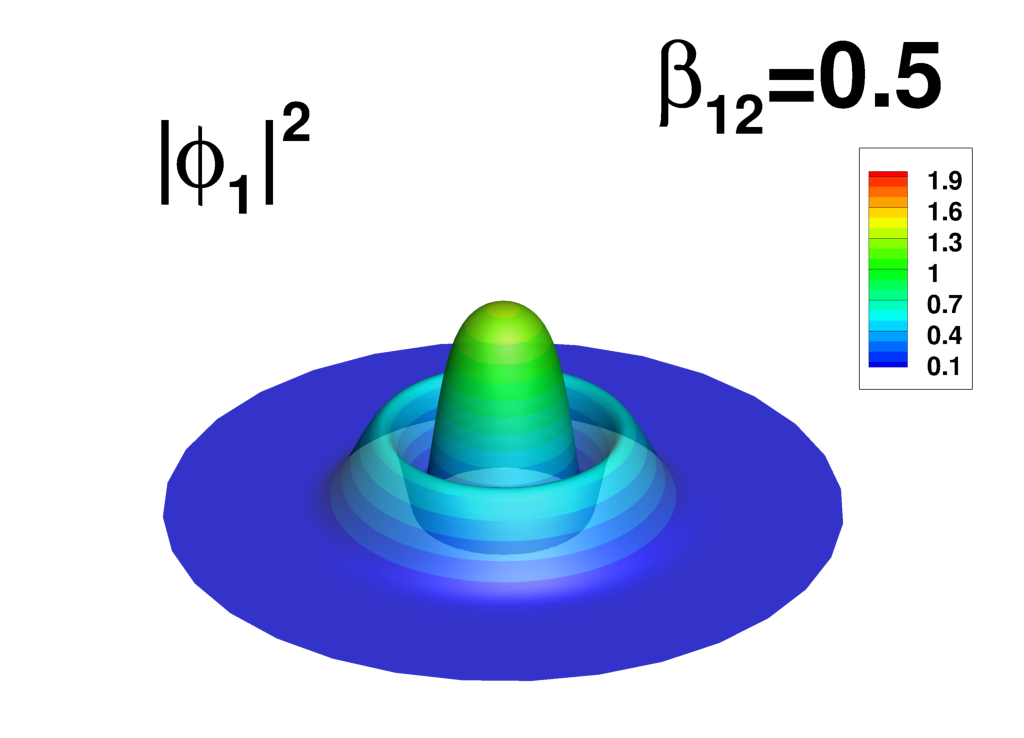 |
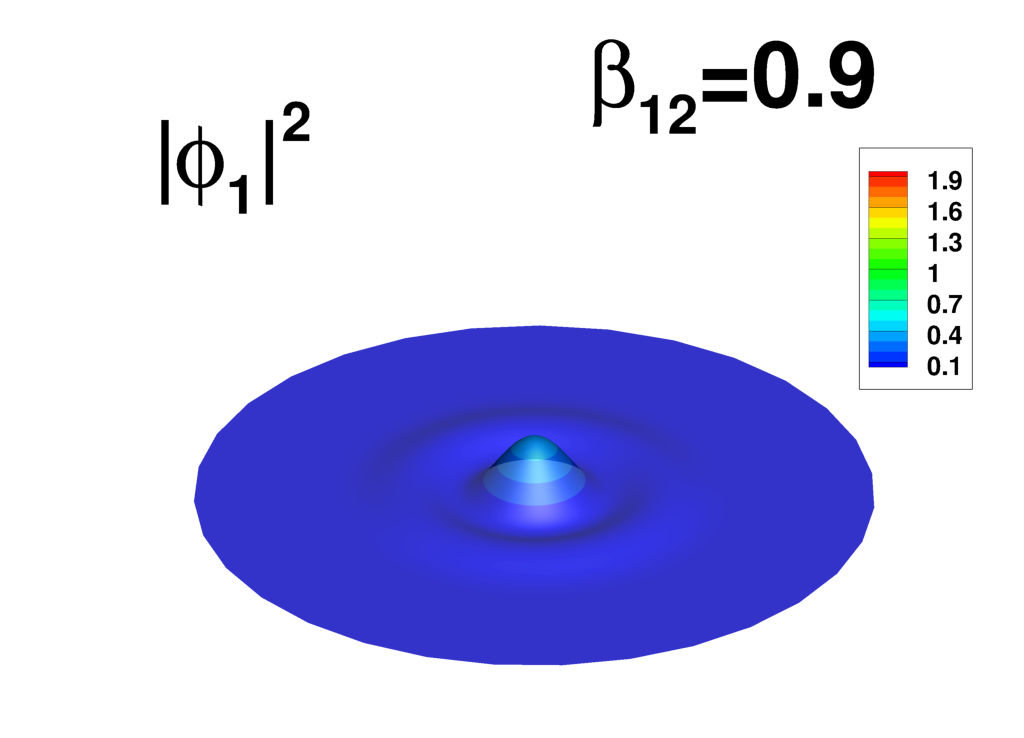 |
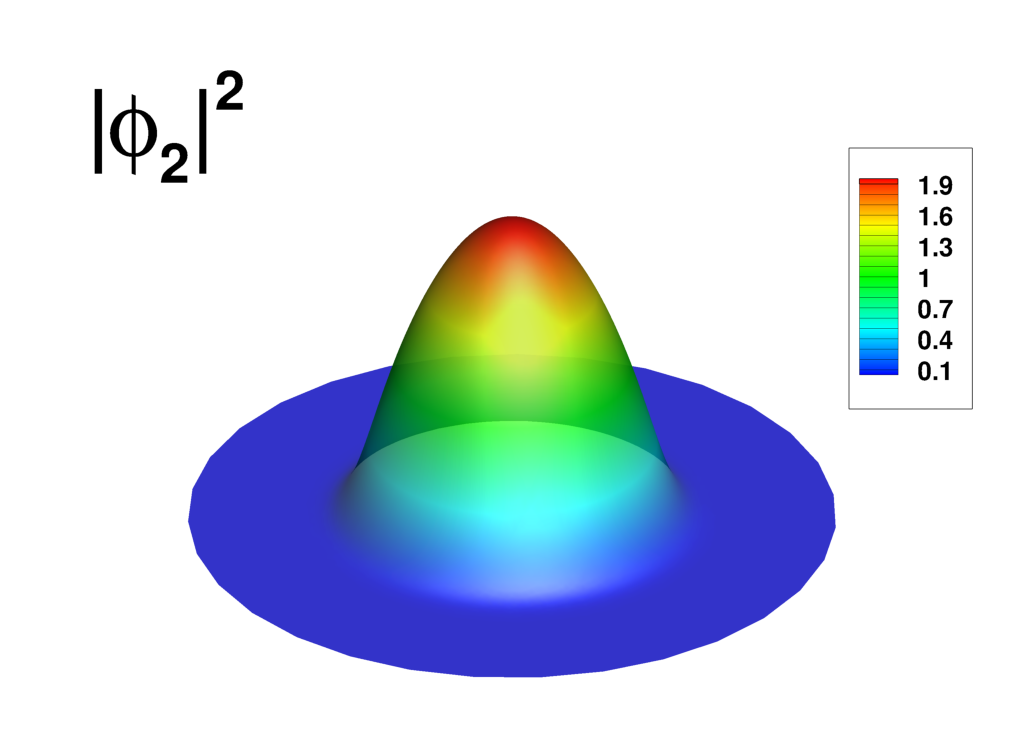 |
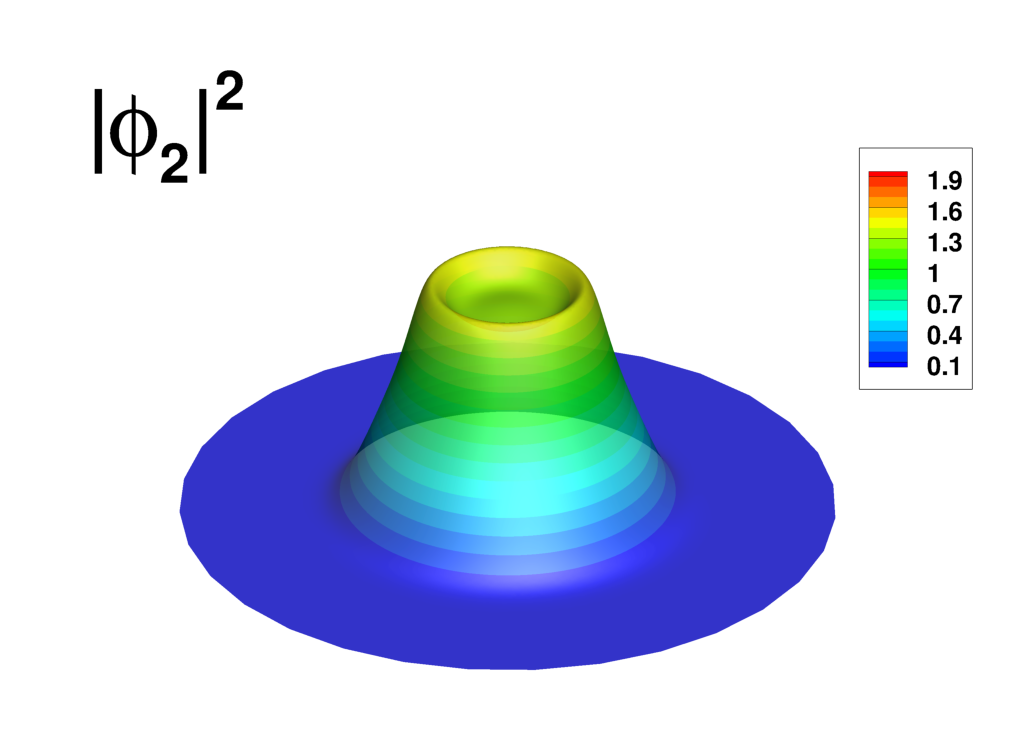 |
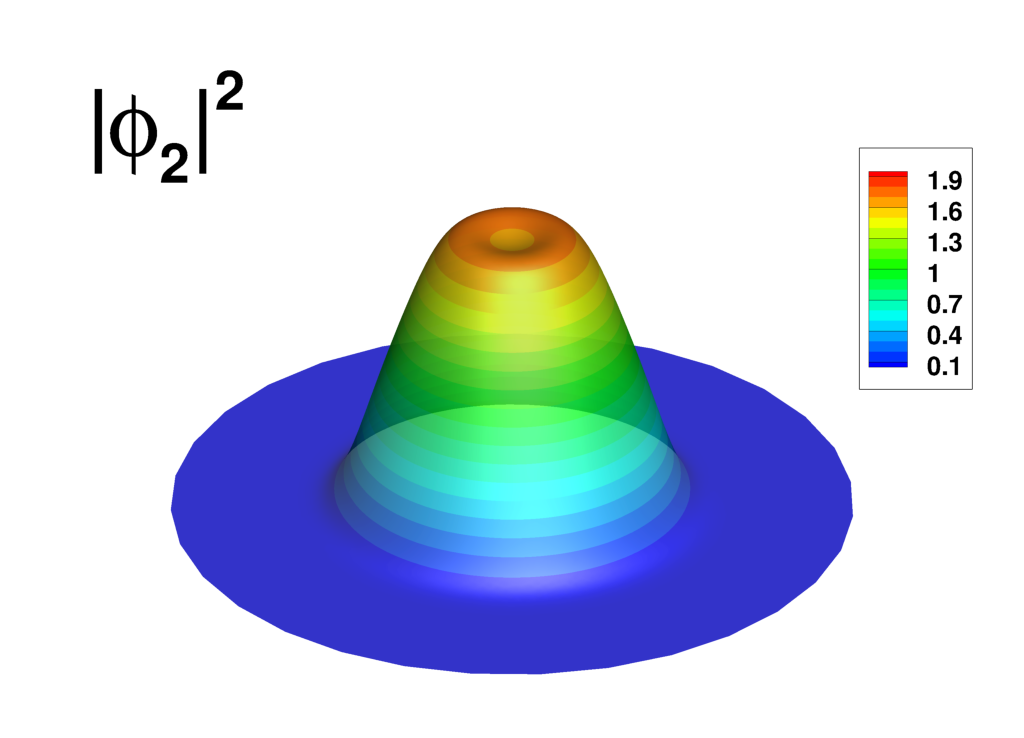 |
Real part $\omega_r$ of eigenvalues
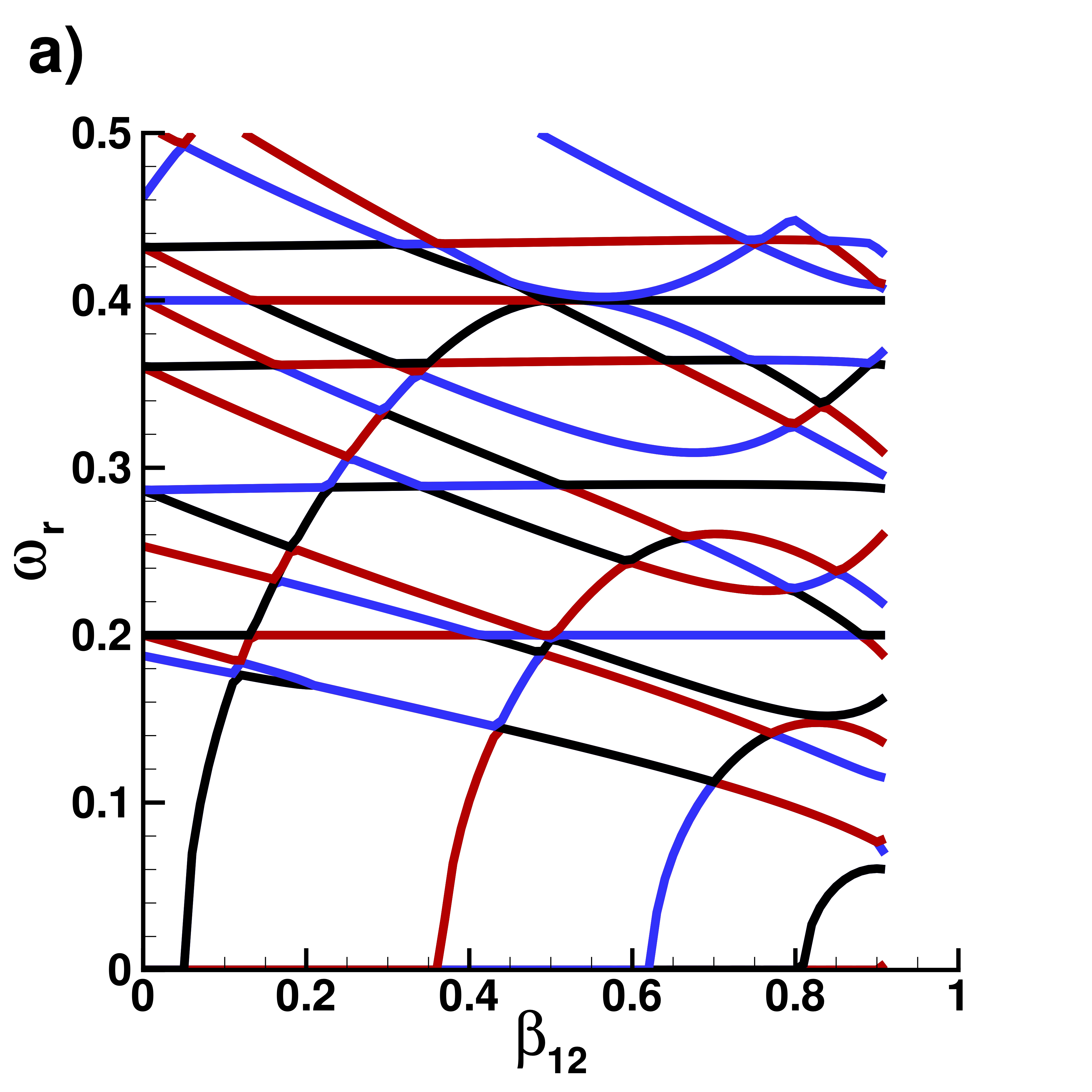 |
Imaginary part $\omega_i$ of eigenvalues
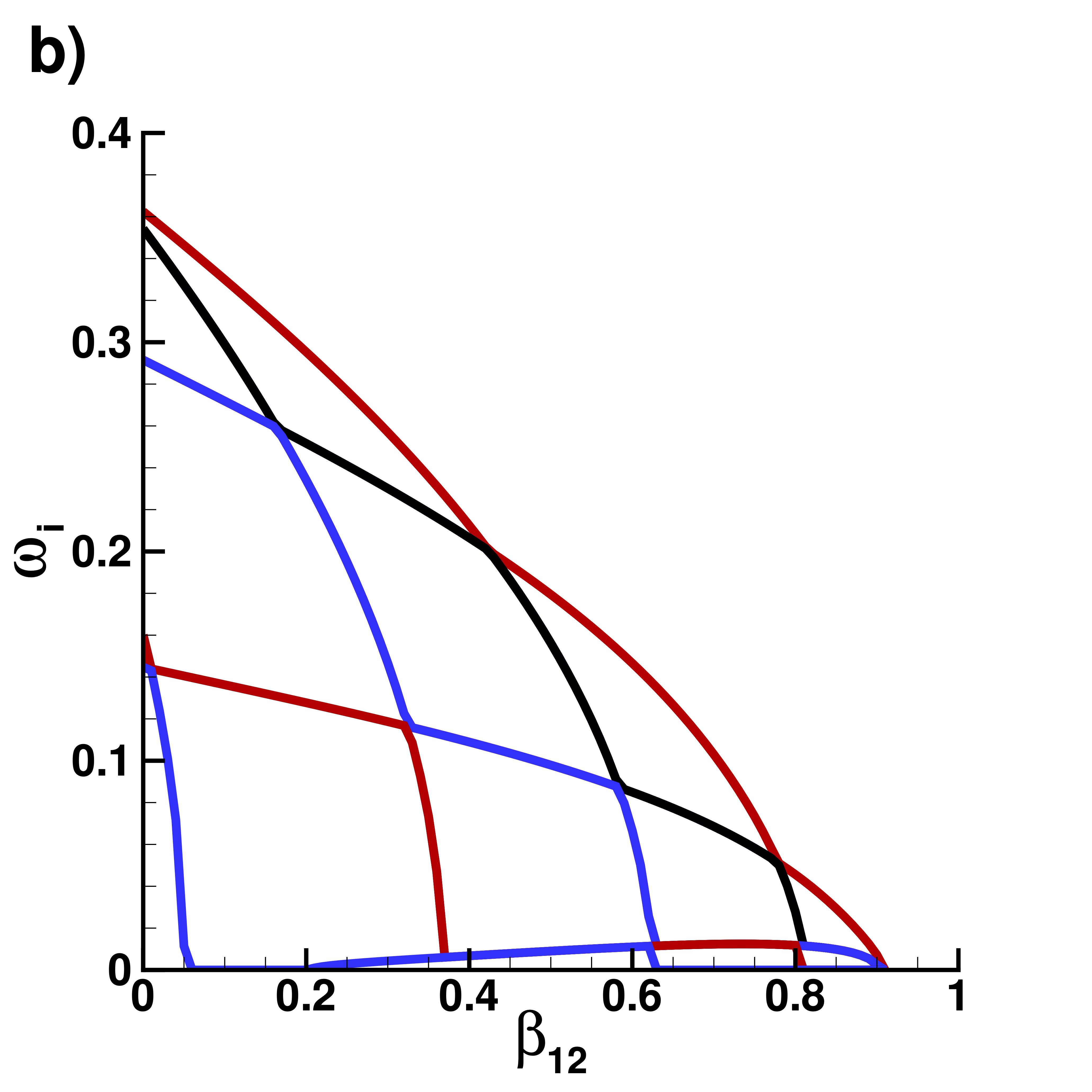 |
Supplemental material: 3D ground state case
Real part $\omega_r$ of eigenvalues
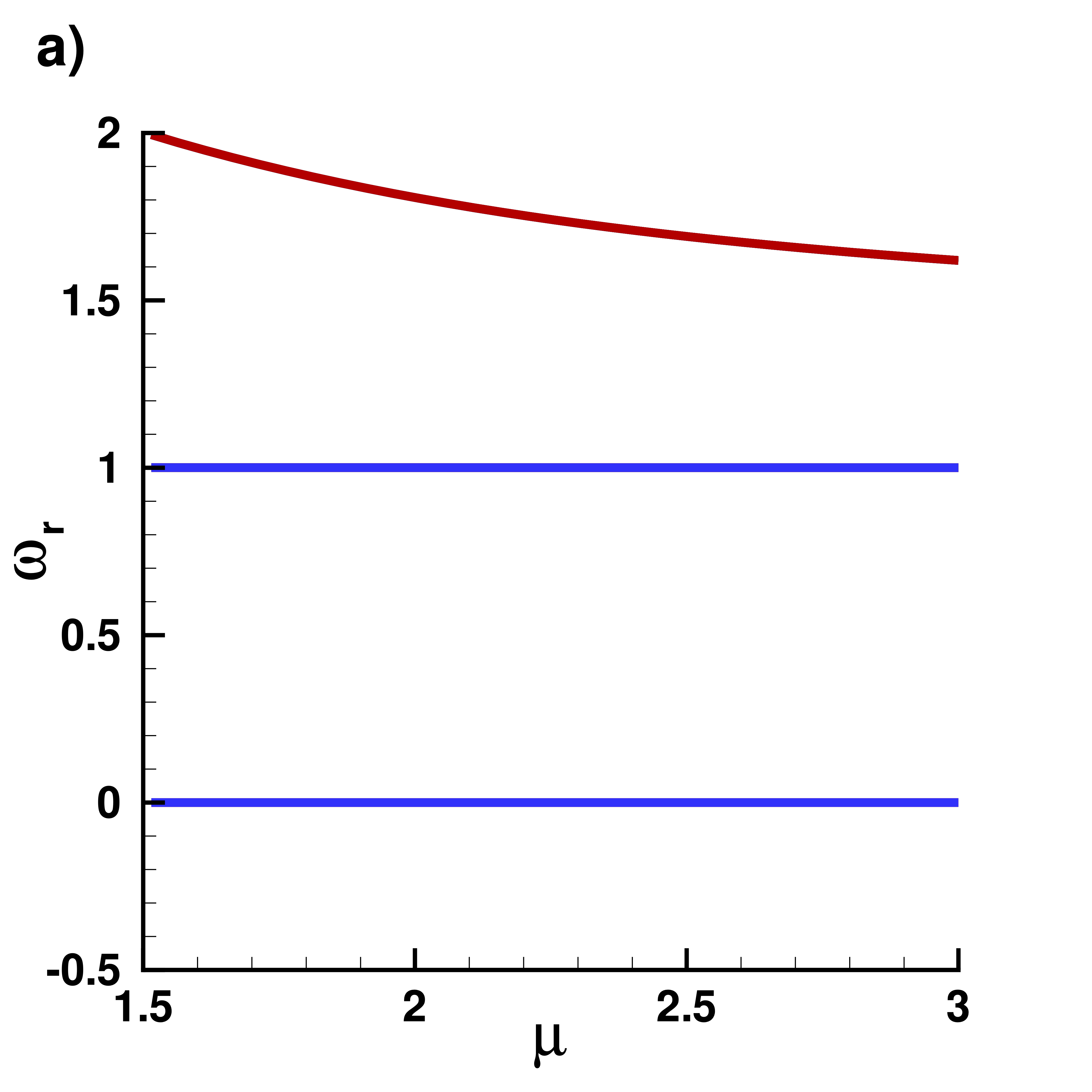 |
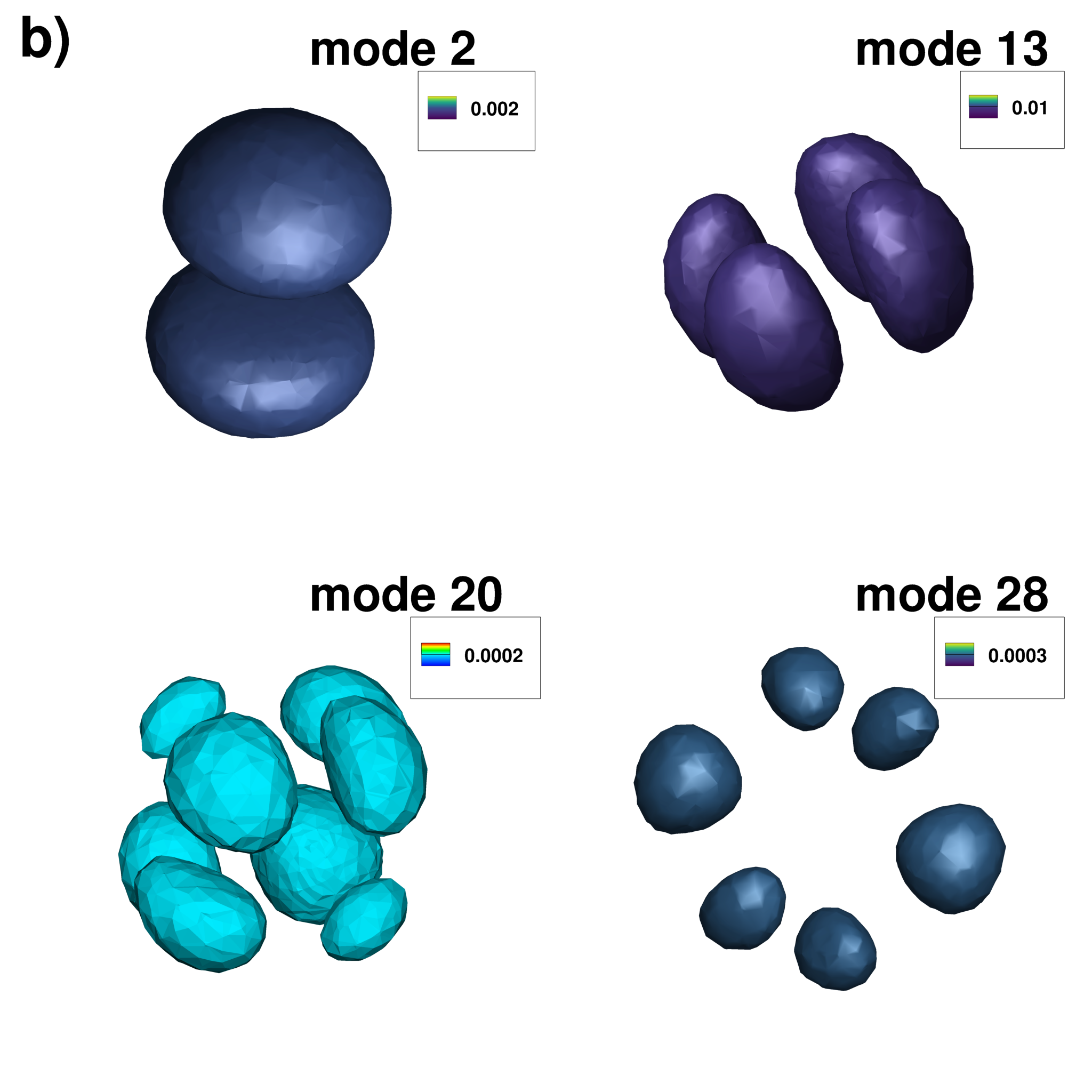
Illustration of four BdG modes (iso-surfaces of the modulus)
 |
